LECTURES 15, 16, 17

Heat exchangers

Heat exchangers are devices where two moving fluid streams exchange heat without mixing.

Heat is transferred from the hot fluid to the cold one.

Under steady operation, the mass flow rate of each fluid stream flowing through a heat exchanger remains constant.

w = 0, Dke = 0, Dpe = 0

Heat exchangers are intended for heat transfer between two fluids within the device.

Usually, the entire heat exchanger is selected as the control volume and Q becomes zero.

Problem: Refrigerant-134a is to be cooled by water in a condenser. The refrigerant enters the condenser with a mass flow rate of 6 kg per min at 1 Mpa and 70^oC and leaves at 35^oC. The cooling water enters at 300 kPa and 15^oC and leaves at 25^oC. Neglecting any pressure drops, determine (a) the mass flow rate of the cooling water required and (b) heat transfer rate from the refrigerant to water.

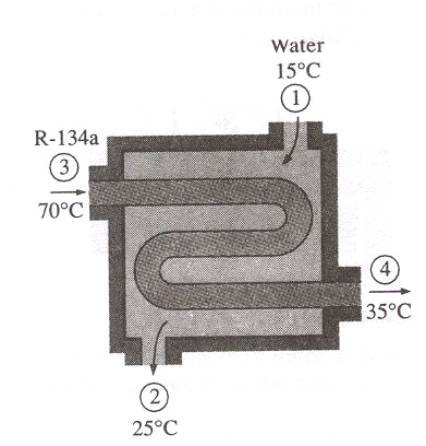
Solution:

Take the entire heat exchanger as the control volume.

h₁ = h_f@15C = 62.99 kJ/kg

h₂ = h_f@25C = 104.89 kJ/kg

The refrigerant enters the condenser as a superheated vapor and leaves as a compressed liquid at 35^oC.

P₃ = 1MPa, T₃ = 70^oC, h₃ = 302.34 kJ/kg.

P₄ = 1MPa, 35^oC, h₄ = h_f@35C = 98.78 kJ/kg

Substituting,

m_w (62.99 – 104.89) = 6(-302.24)

m_w = 29.15 kg/min

(b) Heat transfer from the refrigerant to the water:

Choosing volume occupied by the water as control volume,

Q_w,in + m_w h₁ = m_w h₂

Q_w,in = m_w(h₂ – h₁) = 29.15 (104.89 – 62.99)

= 1221 kJ/min

Mixture chambers

Mixing of two streams of fluids is common in engineering applications.

The conservation of mass for a mixing chamber requires inflow rate to be equal to outflow rate.

w = 0, q = 0, ke = 0, pe = 0

The conservation of energy equation is similar to conservation of mass equation, i.e., energy influx in the control volume is equal to energy outflux from the control volume.

Problem: A small plant has a boiler which produces superheated steam at 3 MPa and 300^oC. It is necessary for a particular process to have saturated steam available at 2 MPa. It is possible to desuperheat the superheated steam by spraying cold water on to it. Suppose the superheated steam enters such a desuperheater at the rate of 1 kg/sec, determine the rate at which spray water at 30^oC and 3 MPa is to be added in the desuperheater.

2 Water, 30^oC

1 3 Sat. Steam 2MPa Sup. Steam

3MPa, 300^oC

Mass balance:

Energy balance:

h₁ = 2995.2 kJ/kg, h₂ = 125.6 kJ/kg

h₃ = 2797.3 kJ/kg, m₁ = 1 kg/s

m₃ = 1+m₂

2995.2 + m₂ (125.6) = (1+m₂)2797.3

m₂ = 0.0741 kg/s

Throttle

Throttle is any kind of flow restricting device that causes a significant pressure drop in the fluid.

The pressure drop does not involve any work.

A large drop in temperature often accompanies the pressure drop in the fluid.

Throttling devices are commonly used in refrigeration and air-conditioning applications.

q = 0, w = 0, Dke = 0, Dpe = 0

Hence across a steady flow throttling device,

h₂ = h₁

Internal energy + flow energy = constant

Joule-Thomson Coefficient

The temperature behaviour of a fluid during throttling process is described by Joule-Thomson coefficient.

m = (¶T/¶P)_h

Joule-Thomson coefficient is a measure of the change in temperature with pressure during a constant enthalpy process.

m_JT <0,temperature increase as the pressure drops

=0, temperature remains constant

>0, temperature decreases

Example:

Steam at 800 kPa, 300^oC is throttled to 200 kPa. Changes in ke are negligible for this process. Determine the final temperature of the steam, and the average Joule-Thomson coefficient.

Control volume: Throttle valve

h_i = h_e

Since h_e = h_i = 3056.5 kJ/kg, and P_e = 200kPa,

These two properties determine the final state.

From superheat table for steam, T_e = 292.4^oC

m_JT (ave) = (DT/DP)_h = -7.6 / -600

= 0.0127 K/kPa

Throttling calorimeter

When wet steam is throttled to a low pressure (usually atmospheric), steam becomes superheated.

The temperature of the superheated steam is measured.

Knowing the pressure and temperature of the steam in the calorimeter, its enthalpy can be determined.

h_e= h_i = X h_g + (1-X)h_f

Knowing the value of h_g and h_f at inlet pressure, X can be calculated from the above relation.

Example:

A throttling calorimeter is used to measure the quality of wet steam in a pipe carrying steam at 2 MPa. The pressure and temperature in the calorimeter are measured as 0.05 MPa and 150^oC. Determine the quality of steam in the mains.

Throttling process is an isenthalpic process. Therefore,

h_i = h_e = 2780.5 kJ/kg

2780.5 = h_f + X h_fg = 908.4 + X (1888.9)

or, X = 0.9911

Uniform flow processes

Some unsteady flow processes can be reasonably represented by simplified model, the uniform flow processes.

1. At any instant during the process, the state of the control volume is uniform (it is the same throughout). The state of the control volume may change with time but it does so uniformly.

2. The fluid properties may differ from one inlet or exit to another, but the fluid flow at an inlet or exit is uniform and steady.

Charging of a cylinder

(m_f – m_o) h_i = m_f u_f – m_o u_o

Further, if the cylinder is initially evacuated, the equation reduces to

h_i = u_f

Discharge of a cylinder

(m_o – m_f) (h + V²/2) = Q + m_o u_o – m_f u_f

Example:

A rigid insulated tank that is initially evacuated is connected through a valve to a supply line that carries steam at 1MPa and 300^oC. Now that valve is opened and the steam allowed to flow slowly into the tank until the pressure reaches 1MPa, at which point the valve is closed. Determine the final temperature of the steam in the tank.

Solution:

We take the tank as the system. This is a control volume since mass crosses the system boundaries during the process. This is an unsteady flow process since changes occur within the control volume. For an evacuated tank, m_o = 0 and m_o u_o = 0. There is only one inlet and no exit.

Assumptions:

1. Uniform flow process. The properties of steam entering the control volume remain constant during the entire process.

2. The ke and pe terms are zero for the tank since it is stationary.

3. The ke and pe of the stream are negligible.

4. w = 0, q = 0

Mass balance:

m_f –m_o = Dm_system

m_o = 0

Energy balance:

E_in – E_out = DE_system

m_oh_o = m₂u₂ (since W = Q = 0, ke = pe = 0 and

m_o = 0)

Combining the mass and energy balances,

u_f = h_i

At P_i = 1MPa and T_i = 300^oC, h_i = 3051.2 kJ/kg

Which is equal to u_f.

Using steam table, at P_f = 1MPa and u_f = 3051.2 kJ/kg, T_f = 456.2^oC.

Alternative solution:

Consider the region within the tank and the mass that is destined to enter the tank as a control mass system as shown in the figure. Since no mass crosses the boundaries, viewing this a control mass system is appropriate.

During the process, the steam upstream (the

imaginary piston) will push the enclosed steam

in the supply line into the tank at a constant

pressure of 1MPa. Then the work done on the

system during this process is

W = -P_i (V_f – V_i) = -P_i (V_tank – (V_tank+V_i))

= P_iV_i

where, V_i is the volume occupied by steam before it enters the tank and P_i is the pressure at the moving boundary (the imaginary piston face)

The energy balance for the control mass system gives

m_i P_i v_i = m_f u_f – m_i u_i

u_f = u_i +P_i v_i = h_i

Example:

A pressure cooker has a volume of 6 litres and an operating pressure of 75 kPa gage. Initially, it contains 1 kg of water. Heat is supplied to the cooker at a rate of 500 W for 30 minutes after the operating pressure is reached. Assuming an atmospheric pressure of 100 kPa, determine,

(a) the temperature at which cooking takes place

(b) the water left in the pressure cooker at the end of the process.

Solution:

Take the pressure cooker as the system. This is a control volume system since mass crosses the system boundaries during the process. This is an unsteady process since changes occur within the control volume.

Assumptions:

1. Uniform flow process.

2. ke and pe are negligible for the escaping steam.

3. Within the pressure cooker, Dke and Dpe are zero. Therefore, DE_system = DU_system

4. The pressure (and thus the temperature) in the cooker remains constant.

5. Steam leaves as a saturated vapor at the cooker pressure.

6. There is no work involved.

7. Heat is transferred to the cooker at constant rate.

(a) The absolute pressure within the cooker is P_abs = P_gage + P_atm = 75 kPa + 100kPa = 175kPa

T = T_{sat@175 kPa} = 116.06^oC

(b)

Mass balance:

m_e = (m_f – m_o)_cv

Energy balance:

E_in –E_out = DE_system

Q_in-m_eh_e = (m_fu_f – m_ou_o)_cv

Combining mass and energy balance,

Q_in = (m_f – m_o)h_e + (m_fu_f – m_ou_o)_cv

The amount of heat transferred during this process is

Q_in = (0.5)(30)(60) = 900 kJ

h_e = h_e@175kPa = 2700.6 kJ/kg

The initial internal energy is found after the quality is determined:

v_o = V/m_o = 0.006/1 = 0.006 m³/kg

x_o = (v_o-v_f)/v_fg = (0.006 – 0.001)/(1.004 – 0.001)

= 0.005

thus,

u_o = u_f + x_ou_fg = 486.8 + (0.005)(2038.1)

= 497.0 kJ

The mass of the system at the final state is

m_f = V/v_f

substituting this in the energy equation,

Q_in = (m_o – V/v_f)h_e + {(V/v_f)u_f – m_o u_o}

There are two unknown in this equation. Assuming saturation conditions exists in the cooker,

v_final = v_f + x_f v_fg = 0.001 + x_f (1.004 - 0.001)

u_final = u_f + x_fu_fg = 486.8 +x_f(2038.1)

Substituting the above in the energy equation, x_f becomes the only unknown.

x_f = 0.009

Thus,

v_final = 0.001 + (0.009)(1.004 - 0.0001)

= 0.010 m³/kg

m_final = V/v_final = 0.006 / 0.01 = 0.6 kg

Therefore, after 30 min, 0.6 kg of water is remaining in the pressure cooker.